RNN(Recurrent Neural Network)이란?
우리가 "나는 오늘 점심으로 맛있는" 까지 읽었을 때, 뒤에 "파스타를 먹었다"가 나올 것을 자연스럽게 예상하는 이유는 앞의 단어들을 기억하고 있기 때문입니다.
순환 신경망(RNN)은 바로 이 아이디어를 흉내 낸 모델입니다. 일반 신경망과 달리, RNN은 순서가 있는 데이터(Sequential Data)를 처리하기 위해 '기억'을 가집니다. 이 기억 장치를 은닉 상태(Hidden State)라고 부르며, 모델은 각 단어를 읽을 때마다 '새로운 단어 정보'와 '이전까지의 기억'을 종합하여 기억을 계속 업데이트합니다.
이처럼 과거의 정보를 다음 단계로 계속 되돌려 보내는(Recurrent) 순환 구조 덕분에, RNN은 문장, 시계열 데이터, 음악과 같이 순서가 매우 중요한 문제를 푸는 데 특화되어 있습니다.
하나의 '가중치(Weights)'로 시퀀스 독파하기
RNN이 문장 전체를 처리할 때, 각 단어마다 새로운 규칙을 적용하는 것이 아닙니다. 대신, 모든 단어를 처리하는 데 단 하나의 동일한 규칙서, 즉 '공유되는 가중치(Shared Weights)'를 반복적으로 사용합니다.
첫 단어를 읽고 기억을 만든 뒤, 두 번째 단어를 읽을 때도 똑같은 가중치를 사용하여 '새 단어'와 '첫 단어의 기억'을 종합합니다. 이 과정을 문장 끝까지 반복합니다. 이 '가중치 공유' 매커니즘 덕분에 RNN은 시퀀스의 길이에 상관없이 동일한 구조로 효율적인 학습이 가능하며, 시퀀스 내의 보편적인 패턴을 학습할 수 있습니다.
RNN 셀(Cell)의 구조
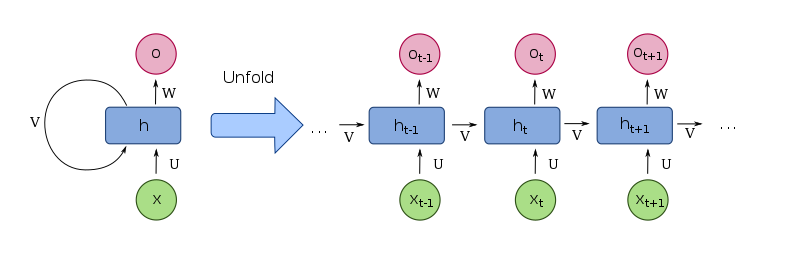
하나의 RNN 셀은 특정 시점 t에서 다음과 같은 입출력 구조를 가집니다.
- 입력 (Input)
- 현재 정보 (xt) : 해당 시점의 새로운 데이터 (예: 문장의 현재 단어)
- 과거 기억 (ht−1) : 바로 직전 시점까지의 정보를 요약한 은닉 상태 - 은닉 상태 (Hidden State)
- 새로운 기억 (ht)
: 현재 정보(xt)와 과거 기억(ht-1)을 종합하여 업데이트된 새로운 은닉 상태.
이 값은 다음 시점으로 전달됩니다. - 출력 (Output)
- 현재 결과 (ot) : 해당 시점에서 내놓는 예측값 (예: 다음에 올 단어 예측)
💡 최초의 기억은 어떻게?
첫 번째 RNN 셀에는 전달받을 과거 기억(h0)이 없습니다.
따라서 이 값은 보통 모든 값이 ‘0’인 '제로 벡터(Zero Vector)'나 아주 작은 랜덤 값으로
직접 초기화해서 사용합니다.
💡 시퀀스 언롤링 (Sequence Unrolling)
실제로는 이 하나의 RNN 셀을 시퀀스의 길이만큼 복제하여
시간 축에 따라 길게 펼쳐놓은 형태로 생각해야 합니다.
이를 '시퀀스 언롤링'이라고 합니다.
위 셀(Cell)의 구조 이미지에서 화살표 우측의 이미지가 언롤링(Unrolling)된 RNN의 모습입니다.
언롤링은 각 시점별 정보의 흐름을 명확히 보여주며, 이후 설명할 학습 과정(BPTT)을 위해 필수적입니다.
RNN의 학습 과정 : 순전파부터 역전파까지
RNN의 학습은 언롤링된 네트워크 위에서 순전파 → 손실 계산 → 역전파(BPTT) 의 과정을 거칩니다.
1. 순전파 (Forward Pass) : 앞에서부터 차근차근 읽기
순전파는 모델이 문장을 처음부터 끝까지 순서대로 읽어나가는 과정입니다.
각 시점(단어)마다 모델은 '현재 단어'와 '이전까지의 기억(은닉 상태)'을 입력받아, '가중치'에 따라 계산하여 '새로운 기억'과 '현재 시점의 예측'을 내놓습니다. 이 '새로운 기억'은 다시 다음 시점으로 전달됩니다.
이 과정이 문장 끝까지 반복됩니다.
2. 손실 계산 (Loss Calculation) : 정답과 비교하며 채점하기
순전파가 끝나면 모델이 내놓은 예측값들과 실제 정답들을 비교합니다.
마치 선생님이 학생의 답안지를 채점하듯, 각 시점의 예측이 얼마나 틀렸는지(오차)를 계산합니다.
그리고 이 모든 시점의 오차들을 합산하여 '총 틀린 점수', 즉 총손실(Total Loss)을 구합니다.
이 총손실 값이 클수록 모델이 잘못 예측했다는 의미입니다.
3. BPTT (Backpropagation Through Time) : 오답노트 작성하기
BPTT는 '시간을 거슬러 올라가는 역전파'라는 뜻으로,
계산된 총손실을 바탕으로 '오답의 원인을 찾아가는 과정'입니다. 모델은 문장의 맨 마지막부터 처음까지 거꾸로 되짚어가며, "이런 큰 오답이 나온 것은 결국 어떤 가중치 때문이었을까?"를 추적합니다.
시간을 거슬러 올라가며 각 시점의 오차에 어떤 가중치가 얼마나 영향을 미쳤는지(기울기)를 계산합니다.
모든 시점에서 동일한 가중치가 사용되었기 때문에, 각 시점에서 계산된 기울기들은 모두 합산되어 해당 가중치를 얼마나 수정해야 할지에 대한 최종 정보가 됩니다.
이렇게 모인 기울기 정보를 옵티마이저(Optimizer)에 전달하여 가중치를 올바른 방향으로 조금씩 수정하며 학습을 반복합니다.
RNN의 한계와 극복 방안
기본적인 RNN은 구조적 한계로 인해 몇 가지 중요한 문제점을 가집니다.
1. 장기 의존성 문제 (Long-term Dependency)
가장 치명적인 문제로, 시퀀스가 길어질수록 초반부의 중요한 정보가 뒤쪽까지 제대로 전달되지 못하고
기억에서 사라지는 현상입니다. 이는 아래 설명할 기울기 문제 때문에 발생합니다.
2. 기울기 소실 / 폭주 (Vanishing / Exploding Gradient)
BPTT 과정에서 동일한 가중치가 반복적으로 곱해지면서,
기울기가 0에 가깝게 사라지거나(소실) 무한대로 커져버리는(폭주) 현상이 발생합니다.
이로 인해 학습이 멈추거나 불안정해집니다.
3. 병렬 연산의 어려움
RNN은 이전 시점의 계산이 끝나야 다음 시점의 계산을 시작할 수 있는 순차적인 구조입니다.
이 때문에 여러 계산을 동시에 처리하는 병렬 연산이 어려워 학습 속도가 느릴 수 있습니다.
해결 방안
게이트 RNN (LSTM · GRU) ✨
정보의 흐름을 통제하는 '게이트(Gate)'를 내부에 두어,
중요한 정보는 오래 보존하고 불필요한 정보는 걸러내어
장기 의존성 문제를 해결하는 가장 근본적인 해결책입니다.
기울기 클리핑 (Gradient Clipping)
기울기가 일정 임계값을 넘으면 강제로 잘라내어 기울기 폭주를 막는 기술적 방법입니다.
Truncated BPTT
역전파의 길이를 일정 수준으로 제한하여 너무 먼 과거까지 기울기가 전파되지 않도록 하는 방법입니다.
RNN의 입출력 구조
One-to-One (기본 회귀/분류)
하나의 입력을 받아 하나의 출력을 내는 가장 기본적인 신경망 구조입니다.
RNN의 핵심인 '순환' 기능을 사용하지 않기 때문에, RNN의 대표적인 활용 사례로 보기는 어렵습니다.
작동 원리 예시
: RNN 셀에 '10시간 공부'라는 입력(x)이 들어가면, 순환 고리(과거 기억)를 거치지 않고 바로 '95점'이라는 출력(y)이 나옵니다. 과거의 기억이 필요 없는 단순한 매핑 작업입니다.
NLU 중심 구조 (이해 및 분류)
Many-to-One (NLU, 분류)
입력 N개 (시퀀스) → 출력 1개
순차적인 데이터를 모두 입력받은 후, 마지막에 단 하나의 결론을 도출합니다.
작동 원리 예시
: "이 영화 정말 최고예요!" 라는 문장을 RNN에 넣습니다. 모델은 '이' → '영화' → '정말' → '최고예요!' 순서로 단어를 읽으며 기억(은닉 상태)을 계속 업데이트합니다. 마지막 단어까지 읽고 난 최종 기억에는 문장 전체의 긍정적인 뉘앙스가 압축되어 있으며, 이 최종 기억을 바탕으로 '긍정'이라는 단 하나의 라벨(One)을 출력합니다.
주요 활용 Task
① 감성 분석
: 영화 리뷰 문장을 읽고 '긍정' 또는 '부정' 라벨을 출력합니다.
② 문서 분류
: 뉴스 기사 전체를 읽고 '스포츠', '정치' 등 카테고리 하나를 결정합니다.
시퀀스 관점
RNN이 “문장 전체”를 끝까지 다 읽도록 순전파를 진행합니다. 중간 단계의 출력들은 모두 무시하고, 오직 마지막 시점의 은닉 상태(final hidden state)만을 사용합니다.
이 '최종 요약 벡터'를 분류기(nn.Linear)에 넣어 단 하나의 결과를 얻습니다.
동기식 Many-to-Many (시퀀스 레이블링, Non-Auto-regressive)
입력 시퀀스의 길이와 출력 시퀀스의 길이가 같고, 각 시점의 입력이 각 시점의 출력과 1:1로 대응됩니다.
작동 원리 예시
: "I love you"라는 문장이 입력되면, 첫 단어 'I'를 읽고 '대명사'라고 출력합니다. 그 다음, 'love'를 읽고 '동사'라고 출력합니다. 이처럼 각 단어를 읽는 매 순간마다, 그 단어에 해당하는 레이블을 즉시 출력하며, 앞선 출력('대명사')이 다음 출력('동사')에 영향을 주지 않습니다. 각 출력이 독립적이므로 이를 비-자기회귀(Non-Auto-regressive) 방식이라고 합니다.
주요 활용 Task
① 품사 태깅: 문장의 각 단어에 "명사, 동사, 조사" 등의 품사를 붙입니다.
② 개체명 인식: 문장의 각 단어가 '인물', '장소', '기관' 중 어디에 속하는지 태깅합니다.
병렬 처리 관점
모든 시점의 출력이 서로 독립적으로 계산될 수 있으므로, 전체 출력 시퀀스를 완벽하게 병렬 처리할 수 있습니다. 이는 매우 빠른 계산 속도로 이어집니다.
NLG 중심 구조 (생성 및 변환)
One-to-Many (NLG, 생성, Auto-regressive)
하나의 '씨앗' 같은 입력을 받아 여러 개의 연속된 데이터(시퀀스)를 출력합니다.
주로 '생성' 작업에 쓰입니다.
작동 원리 예시
: 모델에 '사랑'이라는 단어(One)를 입력하면, RNN은 이 단어를 첫 기억으로 삼습니다. 그 다음부터는 이전 기억을 바탕으로 '고백'을 생성하고, 생성된 '고백'을 다시 입력으로 넣어 '연인'을 생성하는 식으로 연쇄적인 출력을 만들어냅니다. 이처럼 이전 단계의 출력이 다음 단계의 입력이 되는 방식을 자기회귀(Auto-regressive)라고 합니다.
주요 활용 Task
① 이미지 캡셔닝
: 이미지를 보고 "A dog is running" 문장을 생성합니다.
② 텍스트 생성
: '겨울'이라는 주제로 시를 작문합니다.
③ 음악 생성
: '클래식' 장르로 멜로디를 작곡합니다.
병렬 처리 관점
이러한 자기회귀 방식은 한 번에 하나의 토큰만 생성할 수 있어, 출력 시퀀스 전체를 병렬적으로 한 번에 생성하는 것은 불가능합니다. 따라서 생성 속도가 상대적으로 느립니다.
비동기식 Many-to-Many (NLU → NLG, 번역/챗봇)👍
입력 시퀀스를 모두 읽은 후에(NLU), 그 의미를 바탕으로 새로운 출력 시퀀스를 생성(NLG)합니다. 입력과 출력의 길이가 달라도 괜찮습니다.
이 구조를 특별히 Seq2Seq (Encoder-Decoder) 모델이라고 부릅니다.
주요 활용 Task
① 기계 번역
: "안녕하세요" (1개 단어)를 "How are you" (3개 단어)로 번역합니다.
② 챗봇
: 사용자의 질문을 이해하고 답변 문장을 생성합니다.
작동 원리 (Encoder-Decoder)
① 인코더(Encoder) RNN
: 입력 문장 전체를 읽고, 그 의미를 하나의 문맥 벡터(context vector)로 압축합니다. (Many-to-One과 유사)
② 디코더(Decoder) RNN - 자기회귀(Auto-regressive) 방식
: 인코더가 만든 문맥 벡터를 바탕으로, 이전 단계의 출력 단어를 다음 입력으로 삼아 순차적으로 출력 시퀀스를 생성합니다. (One-to-Many와 유사)
병렬 처리 관점
인코더는 입력 시퀀스 전체를 한 번에 처리할 수 있어 병렬화가 용이합니다(특히 트랜스포머 구조에서). 하지만, 디코더는 자기회귀(Auto-regressive) 방식이므로, 출력 단어는 반드시 하나씩 순차적으로 생성해야 합니다. 이 때문에 번역이나 챗봇의 답변 생성 속도에 병목 현상이 발생합니다.
입출력 구조 한눈에 비교하기
| 구조 | 주요 Task | 자기회귀(AR) 여부 | 병렬 처리 | 대표 예시 |
|---|---|---|---|---|
| One-to-One | 기본 회귀/분류 | 해당 없음 | 가능 | 이미지 분류 |
| Many-to-One | NLU (분류) | Non-Auto-regressive | 입력만 가능 | 감성 분석 |
| 동기식 M-to-M | NLU (레이블링) | Non-Auto-regressive | 완전 가능 (입/출력) | 품사 태깅 |
| One-to-Many | NLG (생성) | Auto-regressive | 출력 불가 | 텍스트 생성 |
| 비동기식 M-to-M | NLU → NLG (변환) | Decoder만 Auto-regressive | 인코더만 가능 | 기계 번역 |